第二周
Mini-batch梯度下降
Mini-batch主要是用来处理超大规模的数据,因为每一次梯度下降都需要对所有数据进行处理,所以如果采用full batch的话,那么处理的速度可能很慢,所以此时就将样本进行分割,比如取出1000个样本作为一组,这就是mini-batch,运算结束后再计算下一组。除此之外还有batch梯度下降和stochastic(随机)梯度下降,其中batch就是之前的全部计算,而随机就是将mini batch size设置为1。指数加权平均数(Exponentially weighted averages)以及修正偏差
指数加权平均数的作用是用于提取数据的趋势,因为如果直接使用原数据的话会产生很多的噪音。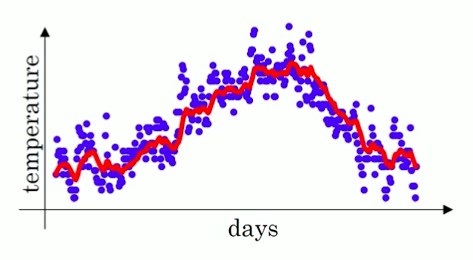
(红色部分为指数加权平均数)
下面给出求指数加权平均数的公式:𝑣𝑡=𝛽𝑣𝑡−1+(1−𝛽)𝜃𝑡
其中β代表之前数据的权重,θt代表当前日期的气温,vt-1代表了前一天的气温。通过上面的推导公式我们知道了第100天的气温是V100=βV99+(1-β)θ100,以此类推我们能得出V99=βV98+(1-β)θ99,由此我们知道V100这个数据实际上是过去的数据的一个总和,只不过随着时间的推进,离得越远的数据其权重越低,我们将V100拓展到近10天的和(β取0.9)为V100=0.1θ100+0.10.9θ99+0.10.92θ98+0.10.93θ97+…+0.10.99θ91+0.910V90。由这个公式我们可以看到等分解到V90时,其权重已经降低到0.910级别,约等于1/e,当权重达到这个级别,我们可以认为后面的数据对于目前的值影响较小,可以不用再考虑,所以说可以用1/(1-β)来表示过去n天的平均温度,比如β取0.9时就能得出过去10天的平均温度,而取0.98时救恩那个得出过去50天的平均温度。
但是用上述方法有缺陷,那就是前期计算的时候,比如V1的值,计算的时候会用到V0的大小,但其实V0值为0,所以本来是40度的温度,可能就变成了4度(β取0.9),所以需要修正偏差,我们使用的方法是计算Vt/(1-βt),其中t代表的累计的数量,比如第t天,β是权重,Vt是修正误差前的数据。计算一下能得出修正后的V1=4/(1-0.9)=40,也就恢复了本来应有的值。动量梯度下降法(Momentum)
计算梯度的指数加权平均数并利用该梯度更新权重。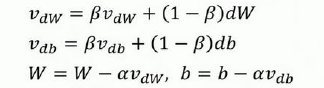
RMSprop和Adam
RMSprop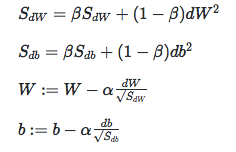
注意dW2实际上是指(dW)2,db2同理。
Adam: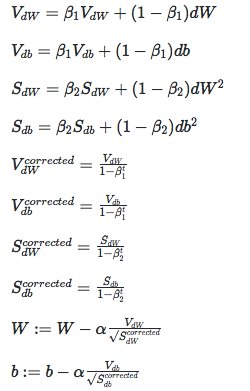
学习率衰减
实际上学习率衰减是为了应对梯度下降的时候出现训练集的损失下降到一定范围后就不再下降的情况,一般的解决方法是线性衰减,例如每过5个epoch就使学习率减半或者指数衰减,例如每过5个epoch将学习率乘以0.1都能起到一定的作用。